Understanding Circle Area Calculation
They appear in nature, design, architecture, engineering, and mathematics. One of the key attributes of a circle is its area, which measures the space enclosed within its boundary. Whether you are a student, engineer, or simply curious about geometry, knowing how to find the area of a circle is a foundational skill.
What Is a Circle?
A circle is defined as the set of all points that are the same distance from a central point. This distance is called the radius, and the center is typically denoted as the point O. The line that passes through the center and touches two opposite points on the circle is known as the diameter, which is twice the length of the radius.
π = Circumference / Diameter
This constant is essential in all circular measurements—circumference, area, and volume of circular objects.
Steps to Find Area
Here is a step-by-step guide to calculate the area of a circle:
Step 1: Measure the Radius
Use a ruler or measuring tool to find the length from the center of the circle to its outer edge.
Step 2: Square the Radius
Multiply the radius by itself. For instance, if the radius is 5 units, then r² = 25.
Step 3: Multiply by π
Now multiply the squared radius by π (you can use 3.14 or 22/7 for practical calculations).
Final Result
You now have the area of the circle in square units (e.g., cm², m²).
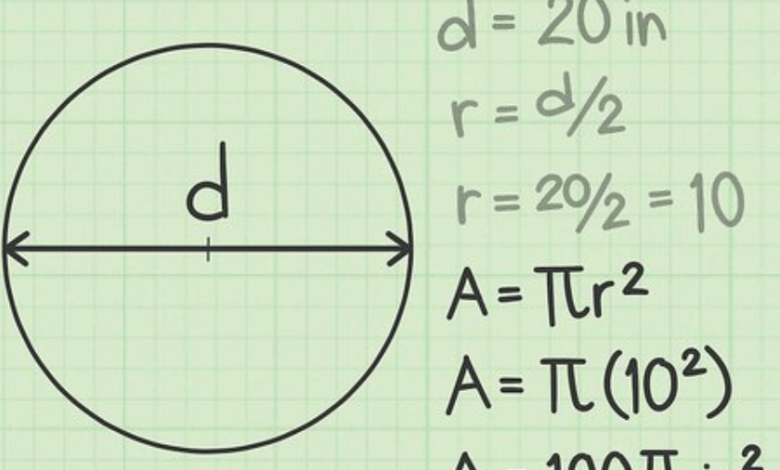
Area Using Diameter
If you know the diameter (d) of a circle instead of the radius, you can modify the formula:
Area = (π / 4) × d²
Since r = d/2, squaring it gives d²/4. Multiply by π and you get the same result.
For example, if d = 10 cm:
A = (π / 4) × 100 = 25π ≈ 78.54 cm²
Pizza
When ordering pizza, the size is usually based on diameter. To compare sizes and value, knowing how to calculate area helps determine how much food you’re actually getting.
See also: How to Advance Your Career as an Arborist
Garden Planning
If you’re planting a circular flower bed or lawn, you need to calculate the area to buy the correct amount of soil or fertilizer.
Common Mistakes
While the formula is simple, there are several mistakes learners often make:
Using Diameter Instead of Radius
A common error is inserting the diameter into the formula directly without halving it. Remember, the area formula requires the radius, not the diameter.
Forgetting to Square the Radius
Make sure you square the radius before multiplying by π.
Ignoring Units
Always include the correct square units in your final answer (e.g., m², ft², cm²).
Circle Area in Coordinate Geometry
If a circle is placed on a Cartesian plane and its equation is known (for example, (x−h)² + (y−k)² = r²), then the radius can be easily identified and plugged into the area formula.
This helps in analytic geometry problems where diagrams are placed on a grid, and calculations are needed based on coordinates.
Circle Segments and Sectors
In some cases, you may not need the entire area of a circle but just a sector (like a pie slice) or a segment (a part bounded by a chord and the arc).
Sector Area Formula:
Where θ is the central angle in degrees.
This is useful in trigonometry, pie chart visualization, and arc-related designs.
Estimating Area Without π
In cases where high precision isn’t necessary, people sometimes estimate area by using rounded values of π like 3.14 or 22/7. However, when precision matters—such as in scientific or engineering work—more accurate values or calculators should be used.
Use of Technology
Calculator
A standard scientific calculator can easily compute the area by entering the radius and using its π function.
Spreadsheet Software
Applications like Microsoft Excel or Google Sheets can automate area computations across multiple entries using formulas like:
=PI() * A1^2
Where A1 is the cell containing the radius.
Programming
Languages such as Python or JavaScript allow you to write scripts that compute areas of multiple circles in just a few lines.
Example in Python:
import math
radius = 7
area = math.pi * radius ** 2
print(area)
Final Thoughts
Mastering how to find the area of a circle equips you with a versatile skill that applies to many academic, professional, and everyday situations. By understanding the simple yet powerful formula A = πr², and being aware of potential errors and extended applications, you can approach a wide range of geometric problems with confidence.




